
前回の記事から、微分積分とは何か、何に使われるのか、ということをご説明しております。
(前回の記事:微分積分とは何か、何に使われるのか① 微分編)
今回はその続き、積分編です。
積分とは何か
前回の記事で微分とは、各瞬間の変化の仕方を示す、ということを説明しました。
復習になりますが、
スタートから3秒までは、1秒で1キロ進み(秒速1キロ)
3秒以降は1秒で2キロ進む(秒速2キロ)
車があるとします。
これを微分する(各瞬間の変化の仕方を示す)と、
スタートから3秒まではY=1(Xが1増えた時のYの増え方は1)
3秒以降はY=2(Xが1増えた時のYの増え方は2)
のグラフとなります。
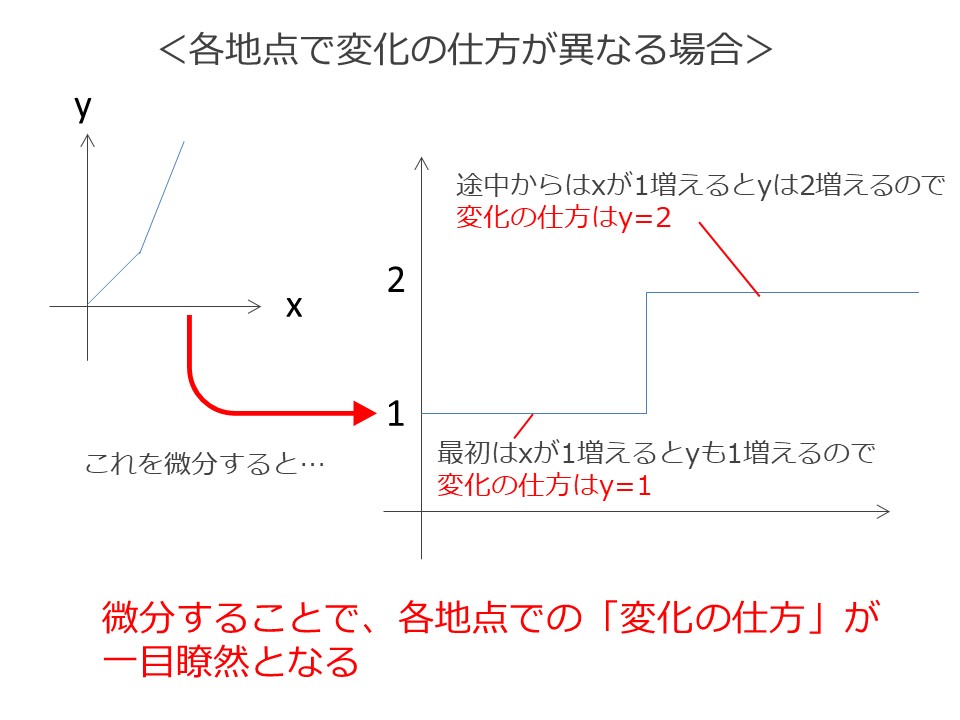
微分によって変化するものの「各瞬間の変化の仕方」を求めましたが、今度は逆に、「変化の仕方から、実際の変化量」を求めてみます。
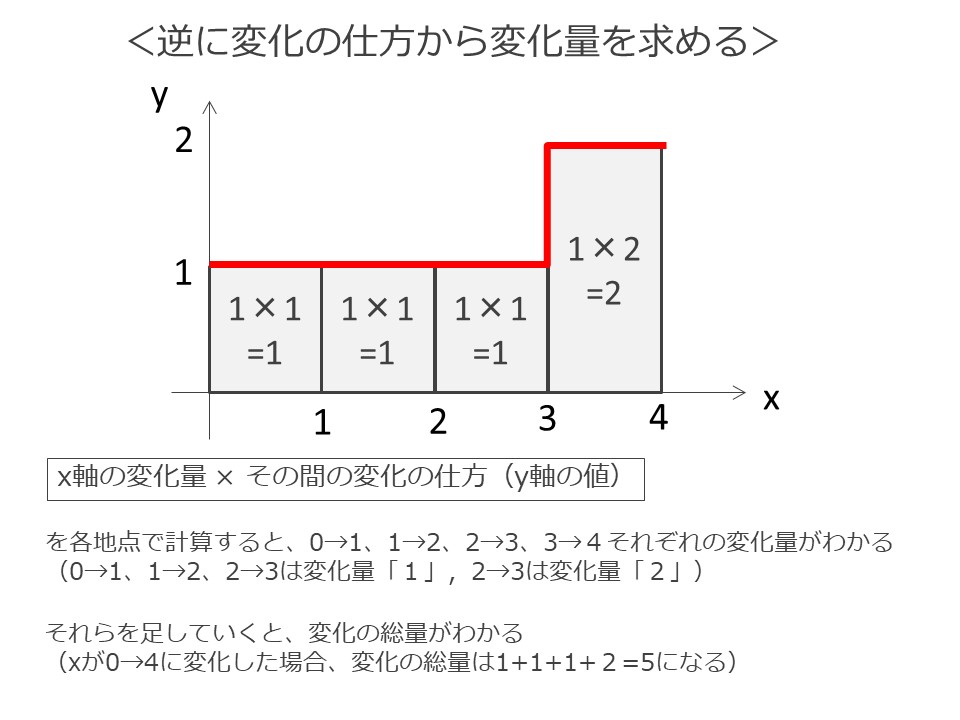
まずは、「X軸の変化量 × その間の変化の仕方」で、その瞬間の変化量を計算します。
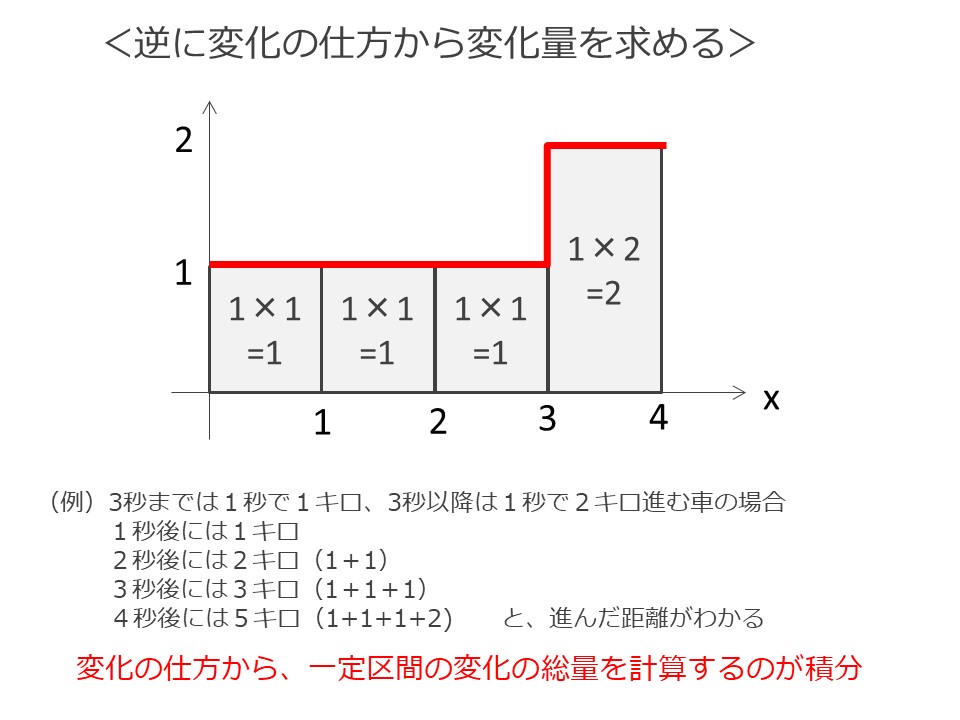
先ほどの車の例でいえば、
スタートから1秒の間は変化の仕方は1なので、変化量(動いた距離)は1×1=1
1秒から2秒の間も変化の仕方は1なので、変化量は1×1=1
2秒から3秒の間も変化の仕方は1なので、変化量は1×1=1
3秒から4秒の間は変化の仕方は2なので、変化量は1×2=2
と、各瞬間の変化量(動いた距離)がわかります。
最後にこれらを足し合わせていくことで、スタートから4秒までの変化量の合計(動いた総距離)がわかります。
1+1+1+2=5キロ 移動した、ということです。
このように、各瞬間の変化の仕方から、その瞬間の変化量を求め、それを足し合わせて一定期間の変化の総量を求めるのが「積分」です。
微分と積分の関係
先ほど説明したとおり、変化の仕方を積分した結果をグラフにすると、そのものの変化の総量(実際の変化量)になります。
変化するものの変化の総量を微分すると変化の仕方を表し、変化の仕方を積分すると変化の総量になります。
つまり、微分と積分は逆の計算を行っているということなのです。
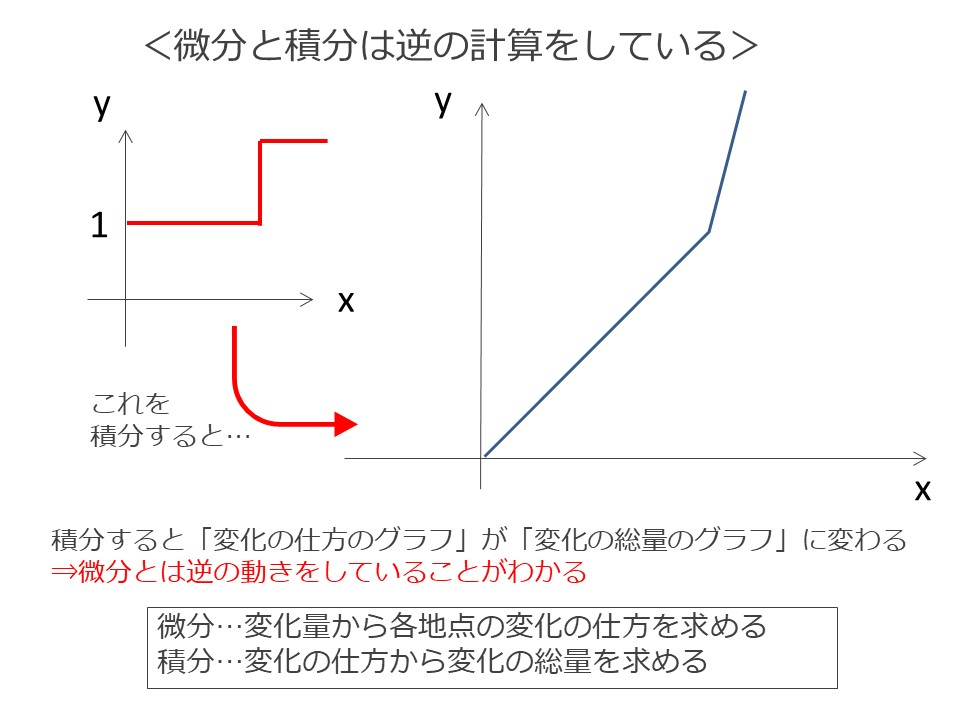
このように、変化の仕方から、実際の変化量を求める「積分」
次は、これがどのように社会で役立っているかご説明します。
積分が何の役に立っているのか
【①自動車の走行距離メーター】
わかりやすい例でいえば、自動車の走行距離メーターがあります。
車の移動速度は各瞬間ごとに少しづつ異なっています。
ここで、各瞬間ごとの速度(変化の仕方)を積分することで、実際に走った距離がわかります。
常に計測している速度を常に積分していくことで、その自動車が走った総距離がわかる、という仕組みです。
【②ドローンの角度】
ドローンには左右に傾いた速度(各速度)を計測する「角速度センサー」が搭載されています。
角速度センサーで計測された各瞬間の変化の速度を積分することで、実際に傾いている量がわかります。
その傾いている量が傾きすぎないように、左右のバランスをとって空を飛んでいます。
直接傾いた量を計測するセンサー(角度センサー)を一緒に搭載してもよいのですが、角速度センサーと角度センサーを両方搭載すると、重くなって飛ぶ効率が悪くなってしまいます。
そのため、角速度センサーのみを搭載し、積分によって傾いた量(角度)を計算しているのです。
これらは積分の使われるほんの一例ですが、
「実際の量(距離)を測ることができない状況で、変化の仕方から総量を計算する」
ということに使われていることがわかります。
同様の状況で、社会の様々な場面で積分が用いられているのです。
積分の成り立ち
最後に、積分の成り立ちについてご紹介します。
もともと積分は、実際に測ることが難しいものの面積を計算で求めることに使われました。
(土地や大仏など)
下の図のように、くねくねしているものは、シンプルに「縦×横」で面積を求めることはできません。
ここで登場したのが積分の考え方です。
くねくねするものを細かく刻んで、細かく刻んだものの面積を計算し、それらを足し合わせていくことで、全体の面積(の近似値)が計算できる、という方法です。
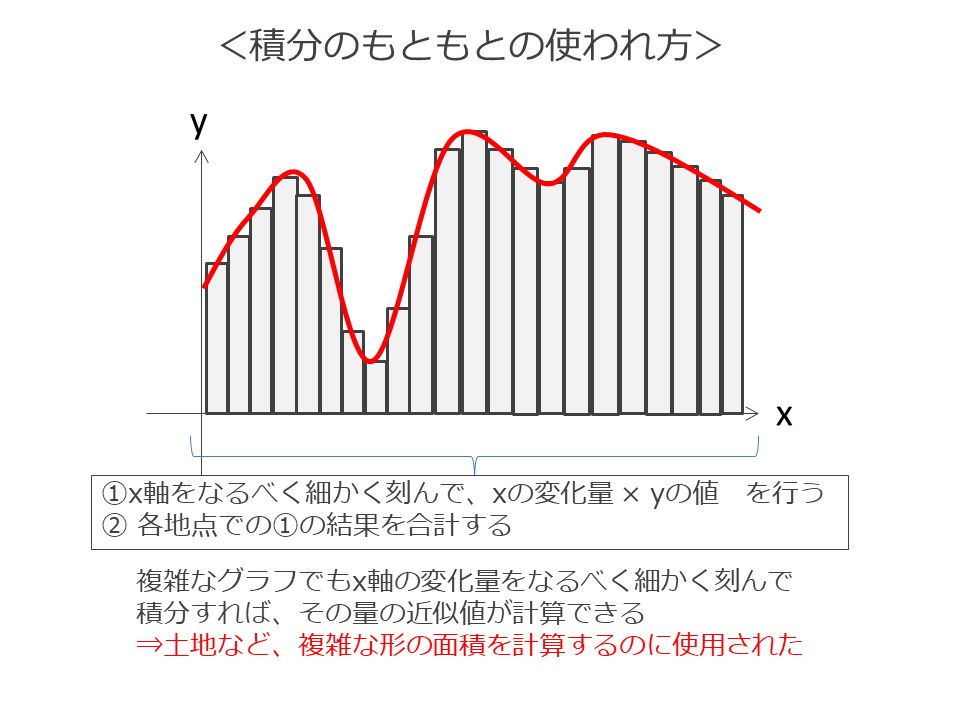
現代の使われ方とは少しことなりますが、「実際に測ることができない量を、変化の仕方から計算で求める」という点では共通しています。
前回と今回にわたり、微分・積分とは何か、何に使われるのか、ということをご紹介しました。
数学の授業では意味が分からなかった微分積分が少しは理解していただけたのではないでしょうか。
また、実際の社会に役に立っていることがわかっていただけると、微分積分を学ぶ意欲がわいてくるかと思います。
