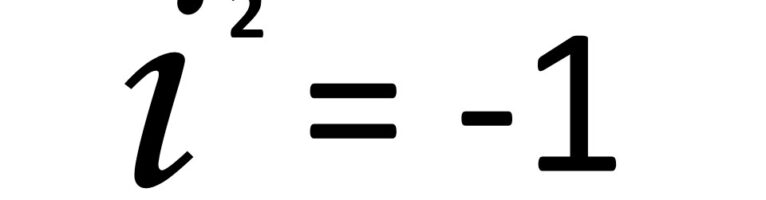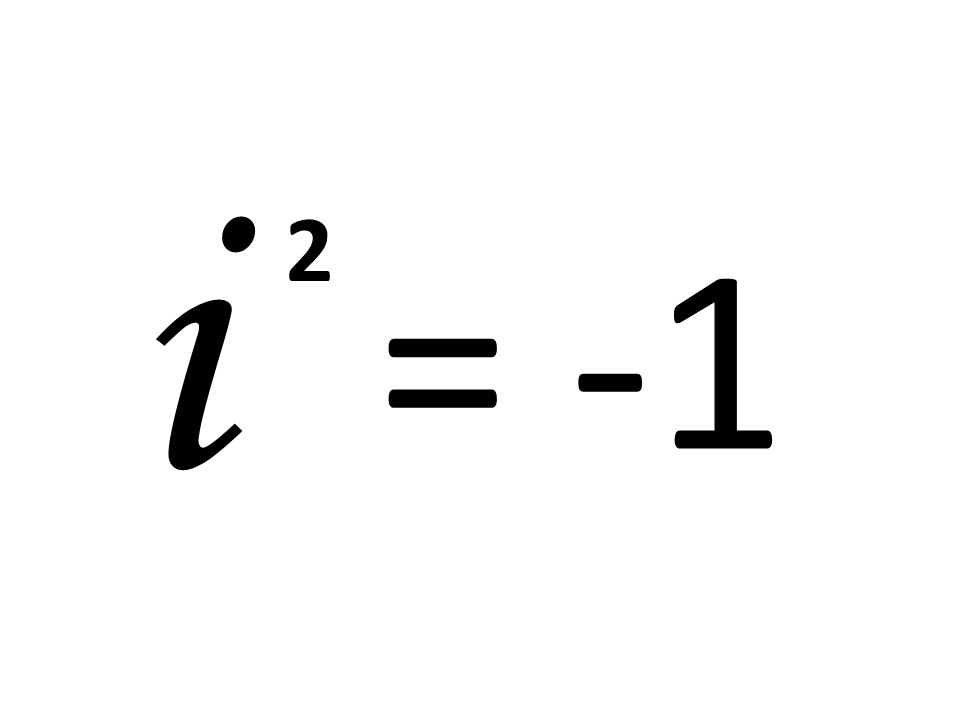
数学において登場する「虚数」という数。
これは簡単に言えば「二乗するとマイナスになる数」のことを指します。
しかし、
1×1=1
-1×-1=1
なので、二乗してマイナスになる数は私たちが普段使う数字としては存在しません。
そこで、「i」という文字を使って、i × i = -1 と表現されています。
このように「存在しない数字」が一体何の役に立つのか、なぜ必要なのか、ギモンに思う方も多いでしょう。
実際、最初に虚数を思いついたカルダノという数学者も、
「計算上あったら便利だが、実社会で役に立つことはない」
ということを述べています。
しかしその後、時代が進むにつれて虚数が実際に役に立つものであることがだんだんとわかってきました。そこで今回は虚数の3つの使い道についてご説明します。
①90°ごとの角度のズレを計算するのに使える
1にiの二乗(=-1)をかけると、答えはー1になります。
それをグラフ上で表現すると、ちょうど180°位置が動いたことを示します。
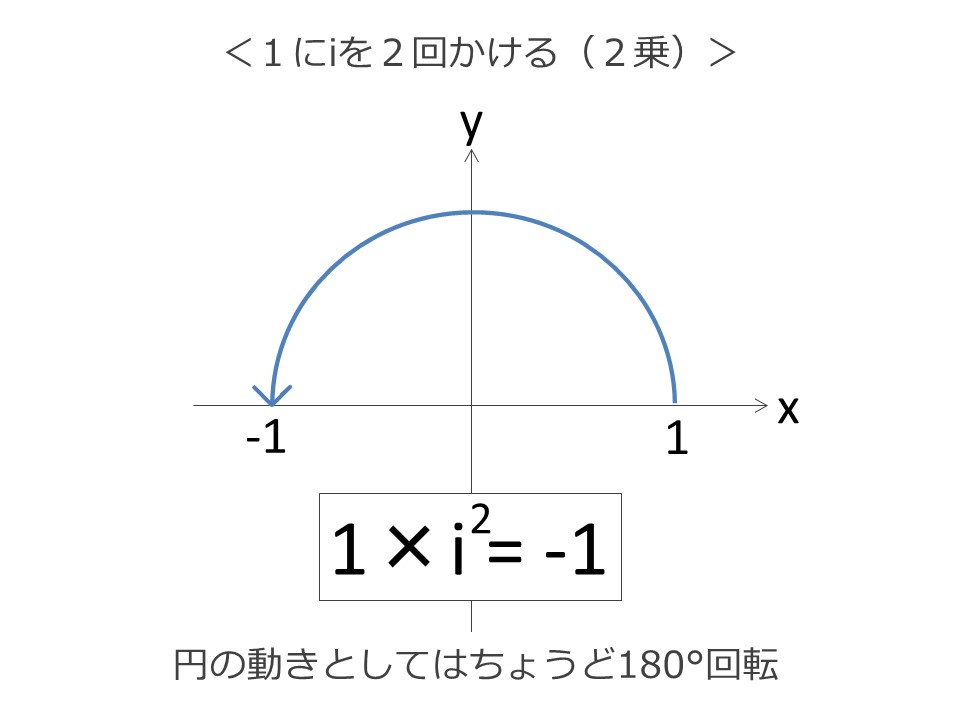
iの二乗、つまり、iを2回かけると180°動くということは、
iを1回だけかけるとその半分の90°動く
と考えることができます。
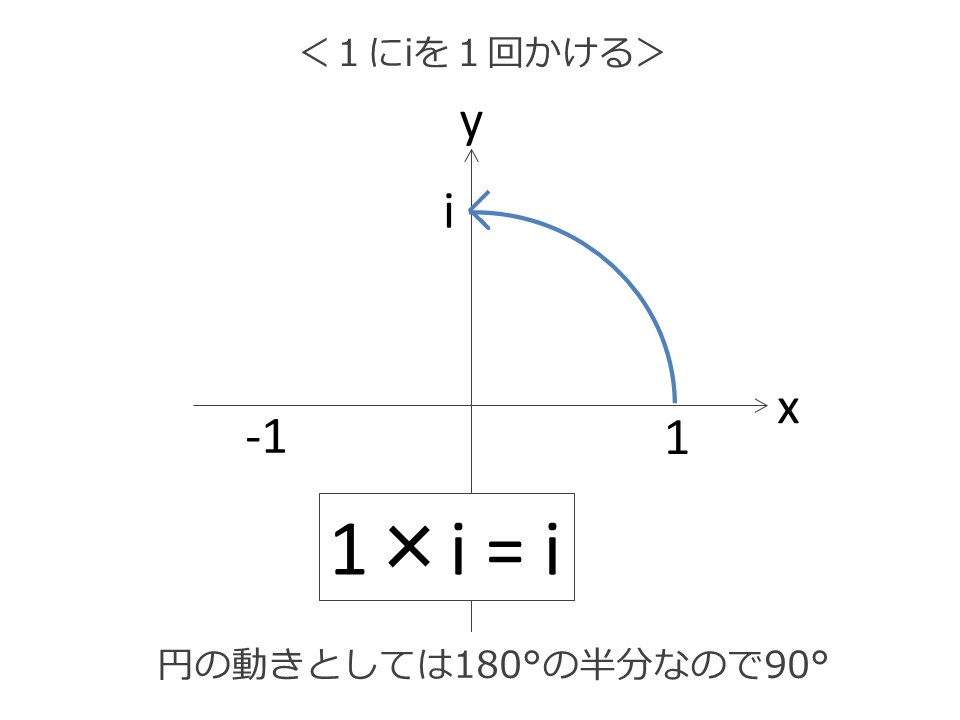
また、iを3回かけると90°×3で270°動いたと考えることができます。
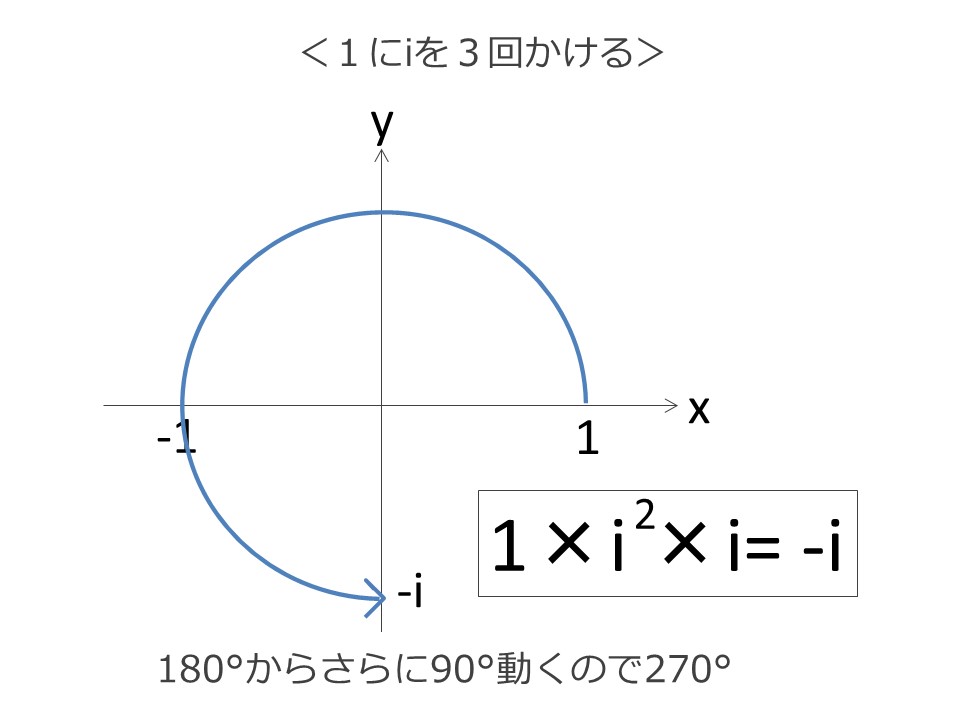
さらにもう1回iをかけて、合計4回iをかけると、-1×-1=1となり、スタート地点に戻ってきます。これは360°動いたことを示します。
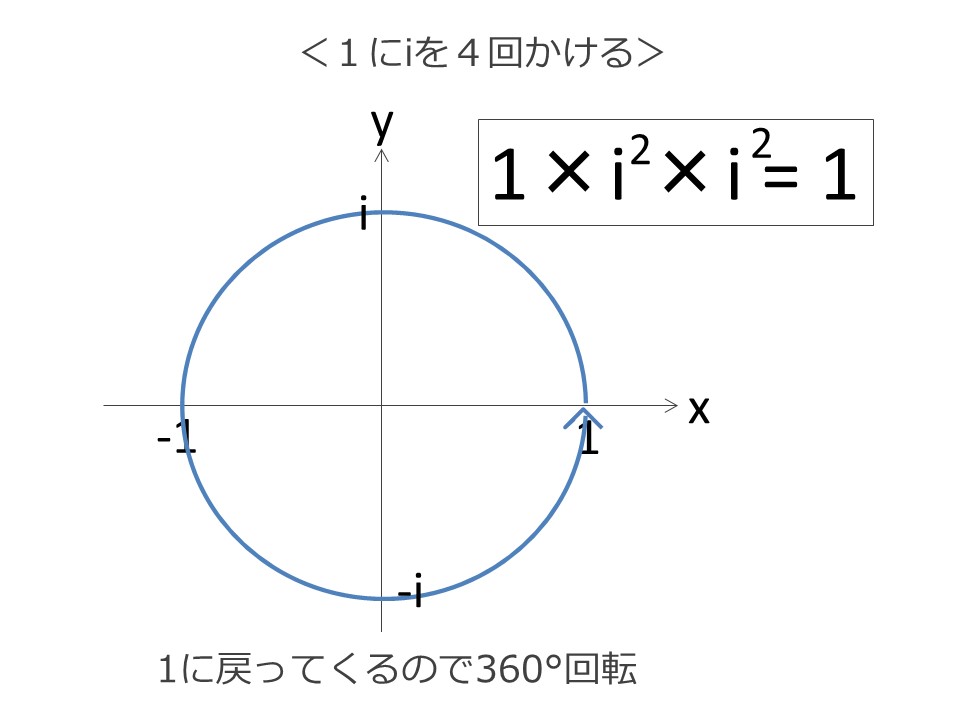
このように、虚数はiを1回かけるごとに90°ずつ移動させることができる、という使い方ができるのです。
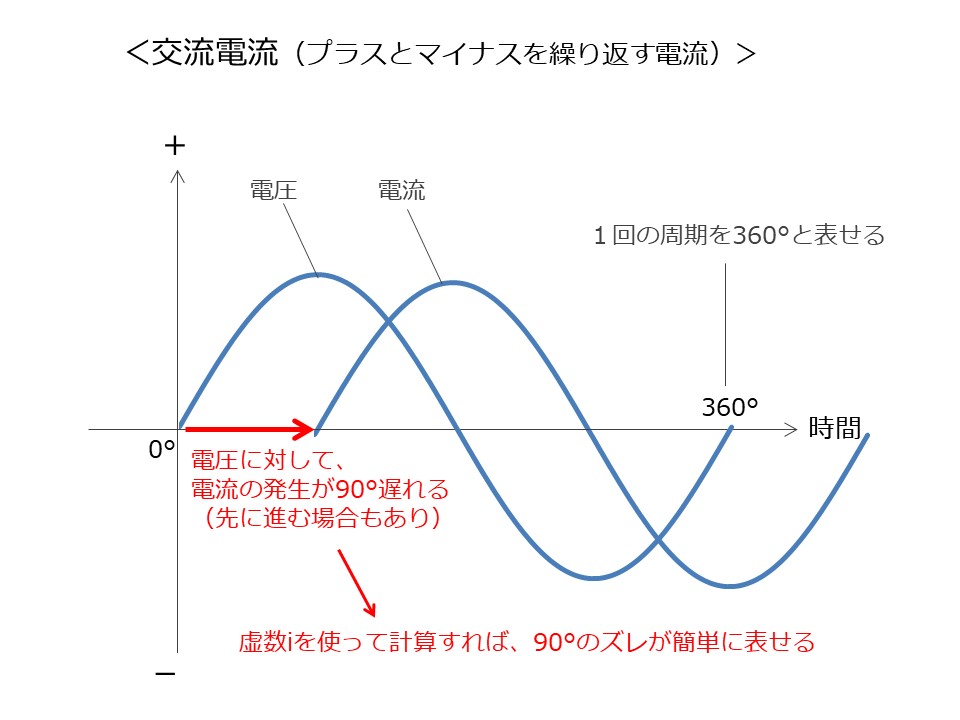
実社会においては、皆さんが普段使っている交流電流(プラスとマイナスを繰り返す電流)において、回路によって、電圧に対して電流が90°遅れたり、進んだりして発生する、という特性があります。
この90°のズレを計算する際に、虚数iを使えば簡単に計算することができます。
しかしこれは「虚数を使うと計算しやすくなる」という話で、必ずしも虚数でなければ計算できないわけではありません。
虚数が必須となってくるのは次の②です。
②原子中の電子が「虚数的な動き」をしている可能性がある
原子とは世の中の物質を構成する最小単位です。
そのうち、「水素」という原子は、中心に原子核を1個、その周りに電子を1個持つ原子です。
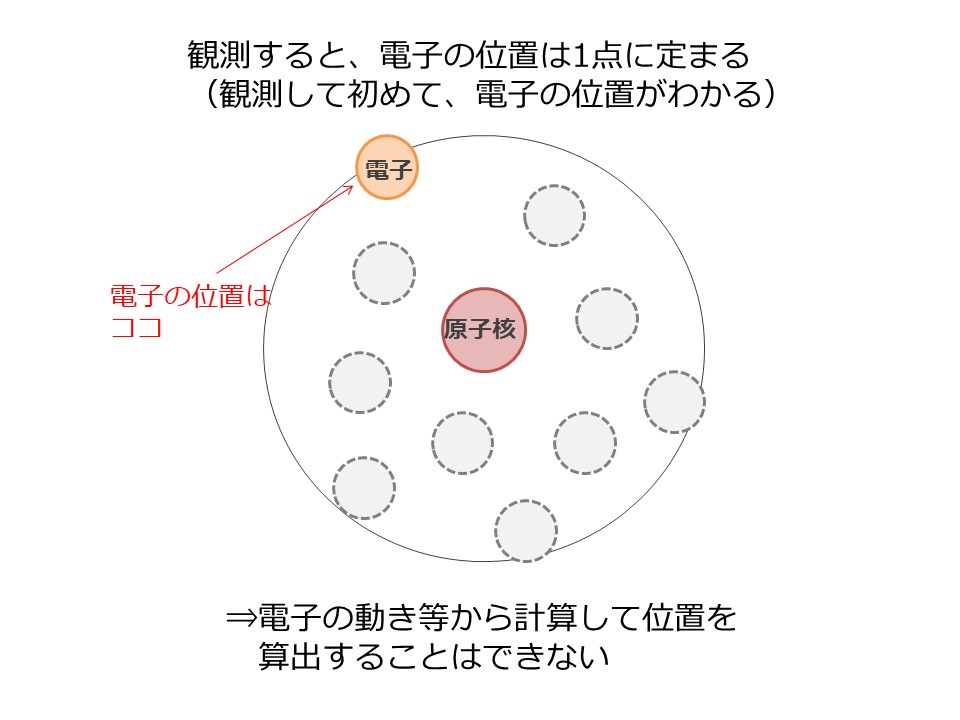
電子はあくまでも1個なのですが、それを観測するまでは、電子は複数の箇所に同時に存在しているという、一般の感覚では理解しがたい、不思議な現象が起こっています。
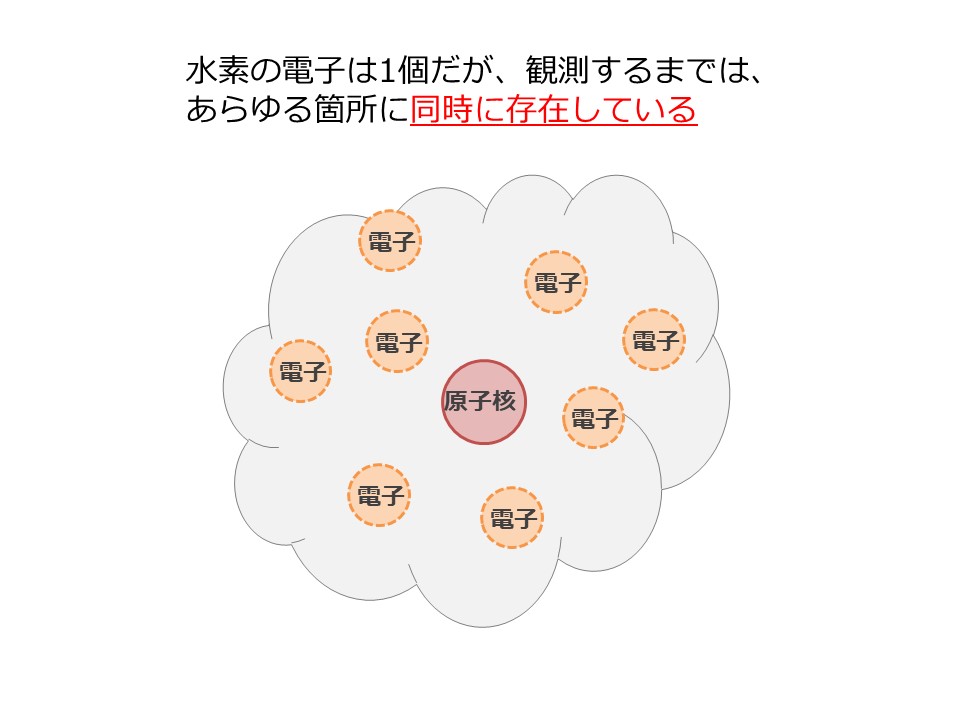
これに光を当てるなどで観測を行うと、そこで初めて電子の位置が一か所に定まります。
つまり、実際に観測しないと位置がわからないので、電子の動きなどから計算して電子の位置を特定することはできない、ということです。
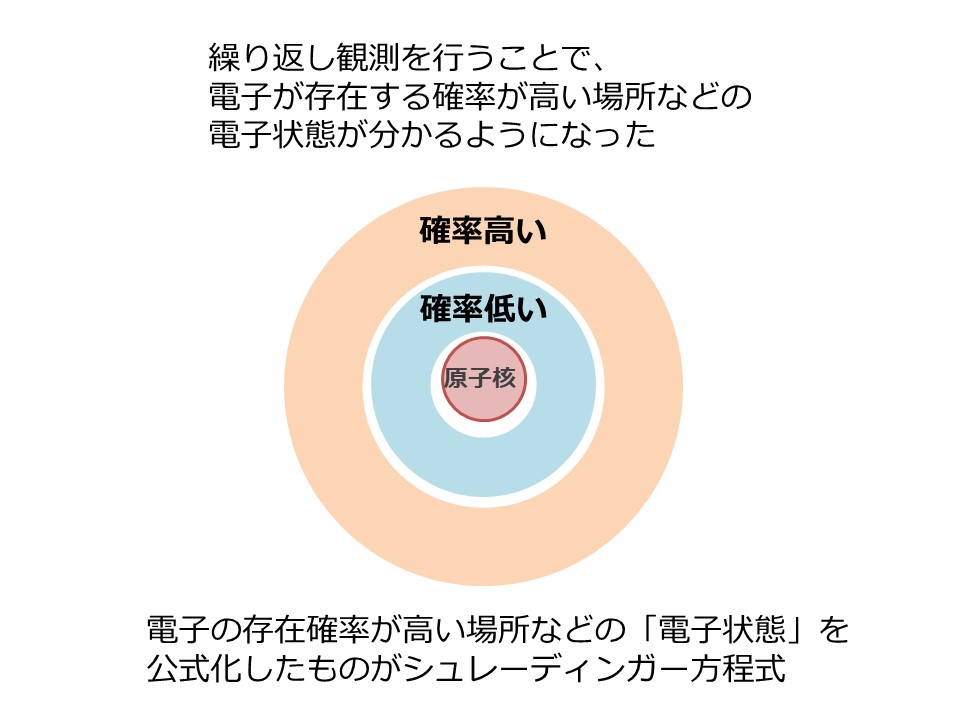
この電子の位置について、観測を繰り返し行うと、電子の存在する確率が高い場所、低い場所がある、といった「電子状態」がわかるようになってきました。
そしてこの電子状態を計算するために公式化されたものが「シュレーディンガー方程式」と呼ばれる公式です。
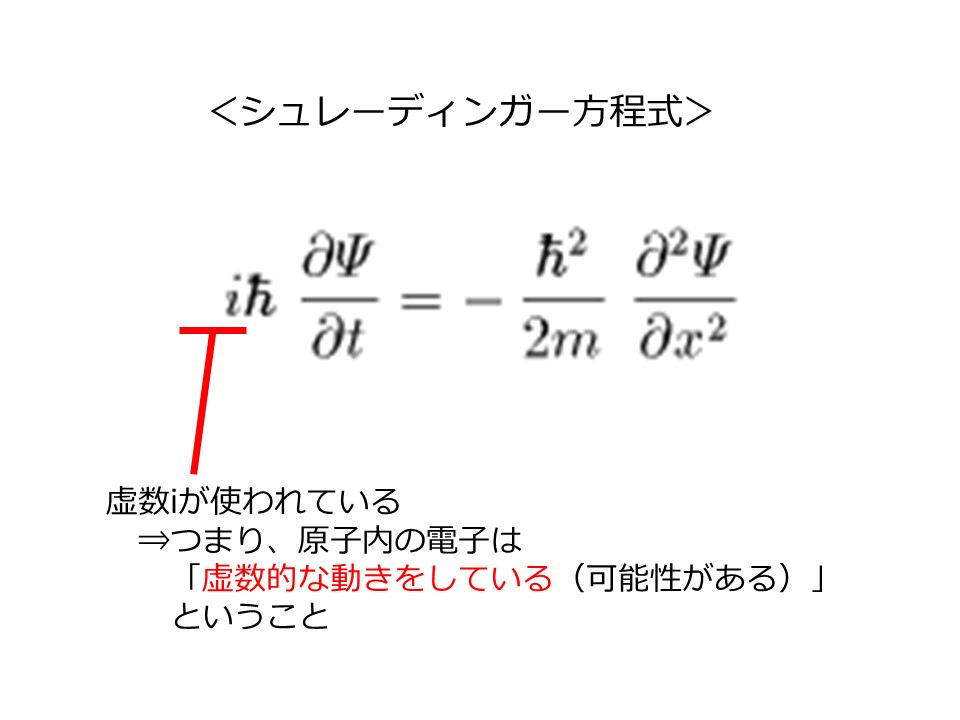
この公式の詳細については管理人は理解できませんが、ポイントは1つ。
この公式には虚数である「i」が使われています。
「i」を使って計算した結果が、実際に観測した結果と一致する、ということは、原子内の電子が「虚数的な動き」をしている可能性がある、ということを示しています。
(イメージとしては、2つが掛け合わさるとエネルギーが減るようなことが起こっているのかもしれない、ということ)
上記のように電子の存在確立が公式化され計算できるようになったことで、電子が従来では考えられなかった箇所に存在し、その電子を通じて超えられないと考えられていたエネルギーの壁を超える現象(トンネル効果)が実用化されるようになりました。
それは例えば電子の移動でデータを保存するフラッシュメモリなど、現実の世界で使われています。
つまり、虚数がなければフラッシュメモリなど電子の移動を用いた製品は実用化されていなかった、ということになります。
③宇宙誕生前に虚数時間が流れていた
最後におまけとして、ホーキングという博士が提唱した、宇宙誕生前は「虚数時間(虚時間)」が流れていた、という説を紹介します。
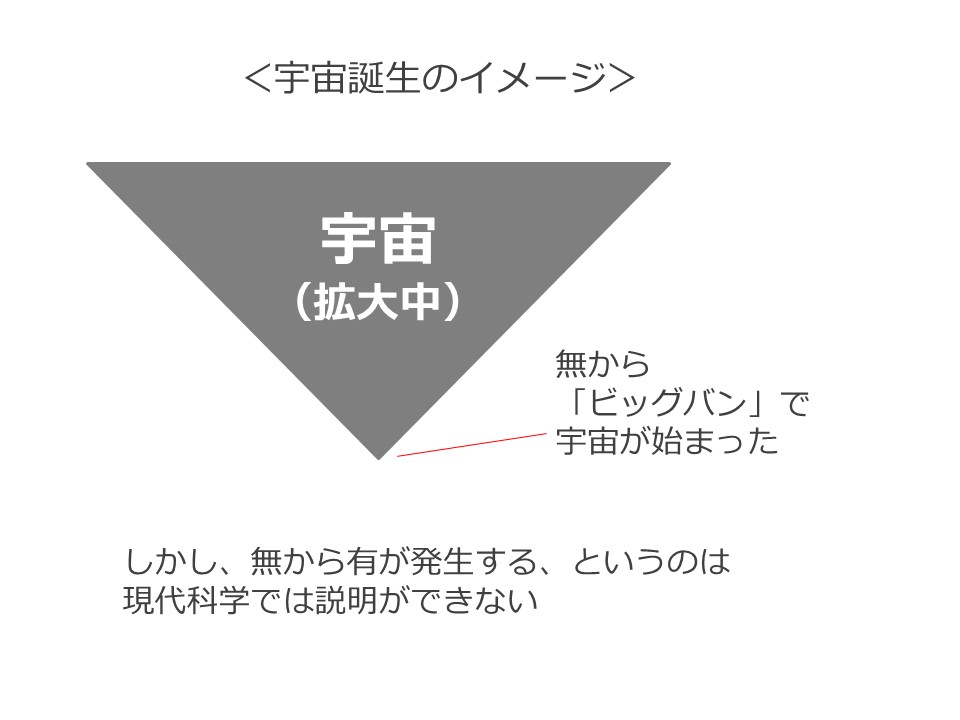
よく知られる宇宙誕生理論は無から「ビッグバン」で宇宙が誕生した、というものです。
しかし、無から有が誕生した、というのはどうもしっくりこず、現代の科学ではなかなか説明がつかないものです。
ホーキング博士はこれを「虚数時間」を使って説明しました。
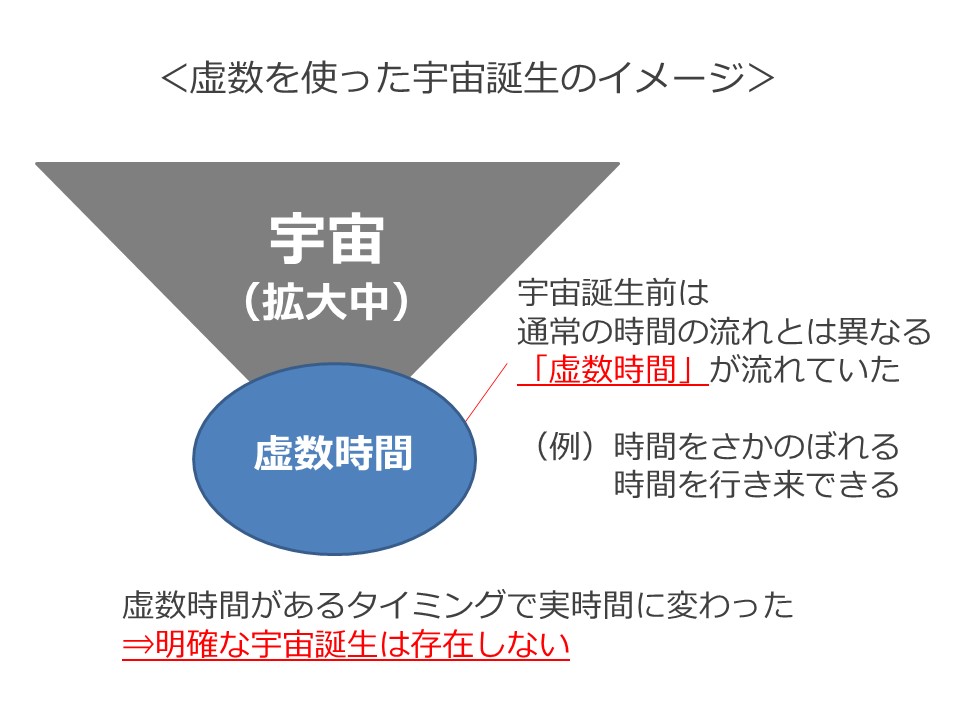
宇宙誕生前は無ではなく、虚数時間が流れていた、といいます。
虚数時間というのは、上手く説明はできませんが、我々が普段体感する時間とは異なる時間の流れ、例えば時間を遡れるとか、自由に行き来できる、とイメージしてください。(二乗するとマイナスになるので、通常の逆の時間が流れる)
その虚数時間が、ある時から実時間に代わり、宇宙が広がり始めた、というだけなので、明確に宇宙の誕生は存在しないということになります。
みなさまの思っている通り、書いている私も何を言っているのかほとんどわかりません。が、現代では説明のつかない事象に「虚数」を当てはめることで説明がつくようになる可能性がある1つの例と言えるのではないでしょうか。
以上、虚数がどのように使われているかについてご説明しました。
数学者からも最初は「実社会で役に立たない数」と言われた虚数が、現代では実社会で使われているということがわかっていただけたでしょうか。
一見何の役にも立ちそうにない「虚数」ですが、こうしたことを少し知っておくだけでも、数学の時間が無駄ではない、将来役に立つ学習なのだ、と思えるのではないでしょうか。