
数学で多くの人がつまづきやすい単元である「微分・積分」
そもそも微分積分って何がしたいのか、何が目的なのか、社会で何の役に立つのか、そうした本質的なことを理解できていないことが、微分積分を難しくしている要因です。
そこで今回は微分積分とは何か、社会で何に使われているか、ということをご説明いたします。
今回は「微分編」です。
微分とは何か
まずは「微分」から説明しましょう。
微分とは、時間によって変化するものの、ある一瞬の変化量(変化の仕方)を表すこと です。
「時間によって変化するもの」の例として、動く車を考えてみます。
この車は常に1秒で1キロ進む、つまり速度は秒速1キロであるとします。
(異常に速いですがそこは気にしないでください)
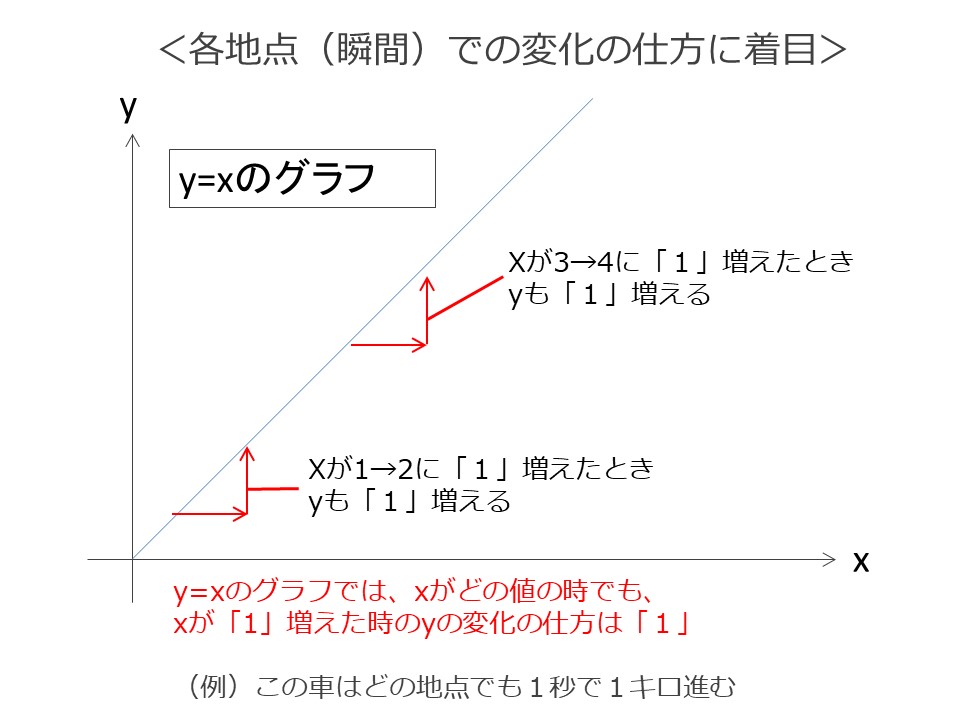
グラフにすると、どの地点でもX(時間)が1増えたとき、Y(距離)も1増えることになるので、右肩上がりのまっすぐなグラフになります。
Xが1→2に増えた時も、3→4に増えた時も、どの地点でもYの増え方は1です。
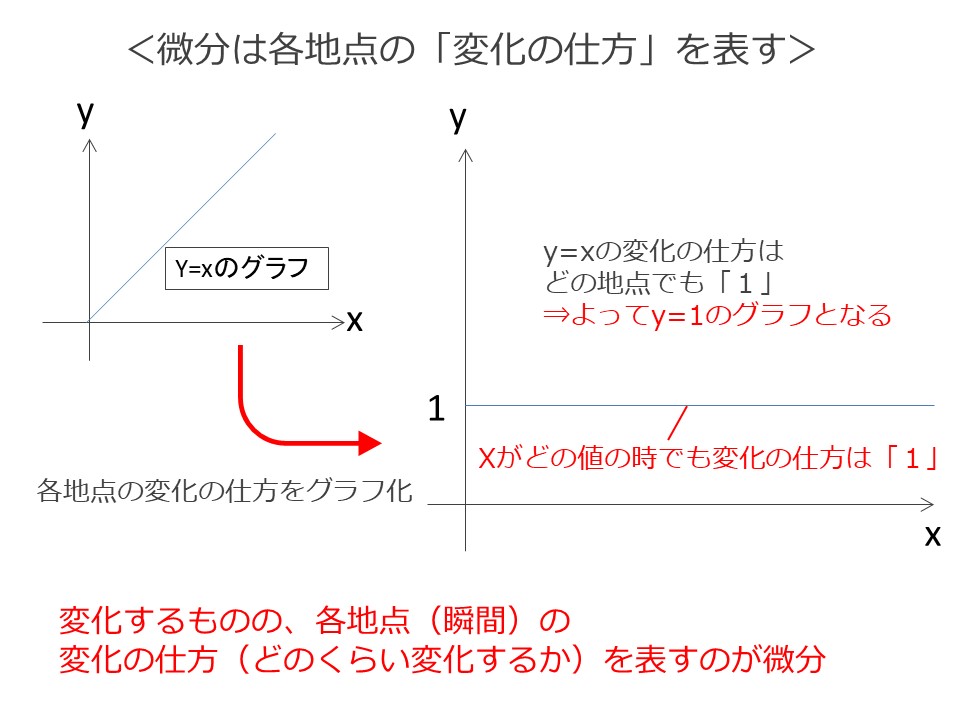
ここから、この車の「各瞬間の変化の仕方」をグラフにしてみます。
変化の仕方はXがどの値の時でも必ず「1」なので、Y=1のグラフ(横にまっすぐなグラフ)となります。
⇒この車はスタートからゴールまで、常にXが1増えたらYが1増える、一定の速度で走り続けたことを示しています。
このように、変化するものの「各瞬間の変化の仕方」を表すことが「微分する」ということなのです。
ちなみに、各瞬間の変化の仕方を調べるために、Xを「細かく分ける」ので「微分(微に分ける)」と呼ばれます。
(上記例の場合はXの変化量を1ずつに分けましたが、実際はもっと細かく分けていきます)
理解を深めるため、もう1つ別の例で考えてみましょう。
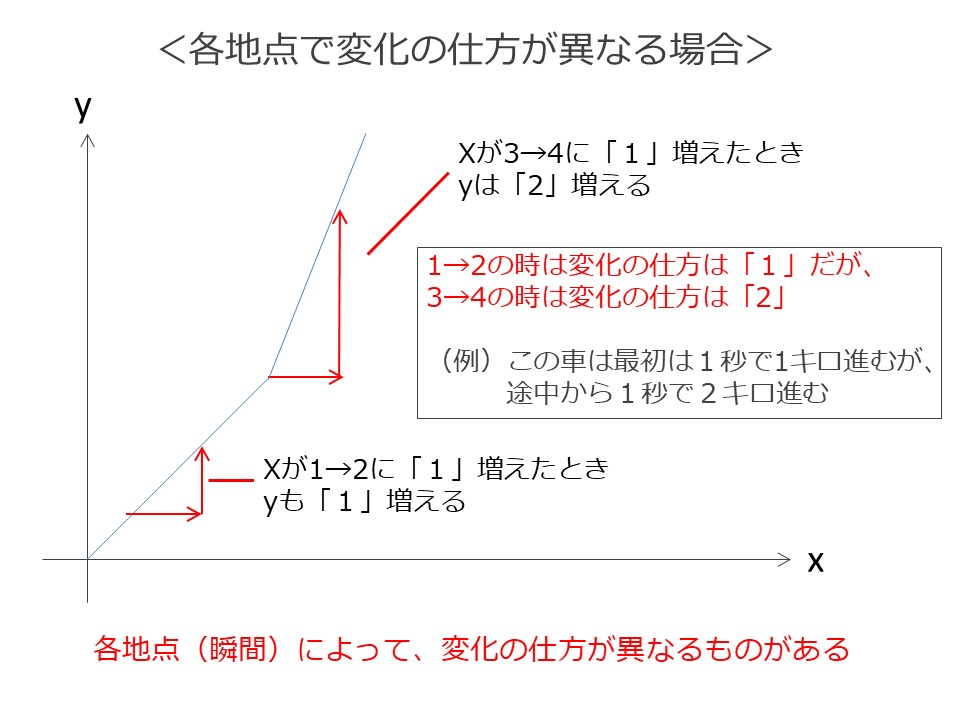
下のグラフの車は、
スタートから3秒までは1秒に1キロ進む(秒速1キロ)
3秒以降は1秒に2キロ進む(秒速2キロ)
という進み方をする車です。
よって、X(時間)が1→2に増えた時はYは1増え、3→4に増えた時はYは2増えるということです。
最初の例ではXがどの値の時でも(全ての瞬間で)Yの増え方は一定でしたが、今回の場合はXの値によって(瞬間ごとに)Yの増え方が違う、ということがポイントです。
世の中のものは、このように各瞬間によって変化量が異なるものがほとんどです。
これを、各瞬間の変化の仕方を表すグラフに変換、つまり微分してみます。
スタートから3秒まではXが1増えた時のYの増え方は1、つまりY=1のグラフとなります。
3秒後からはXが1増えた時のYの増え方は2、つまりY=2のグラフとなります。
よって、以下の図のように、階段のようなグラフになるわけです。
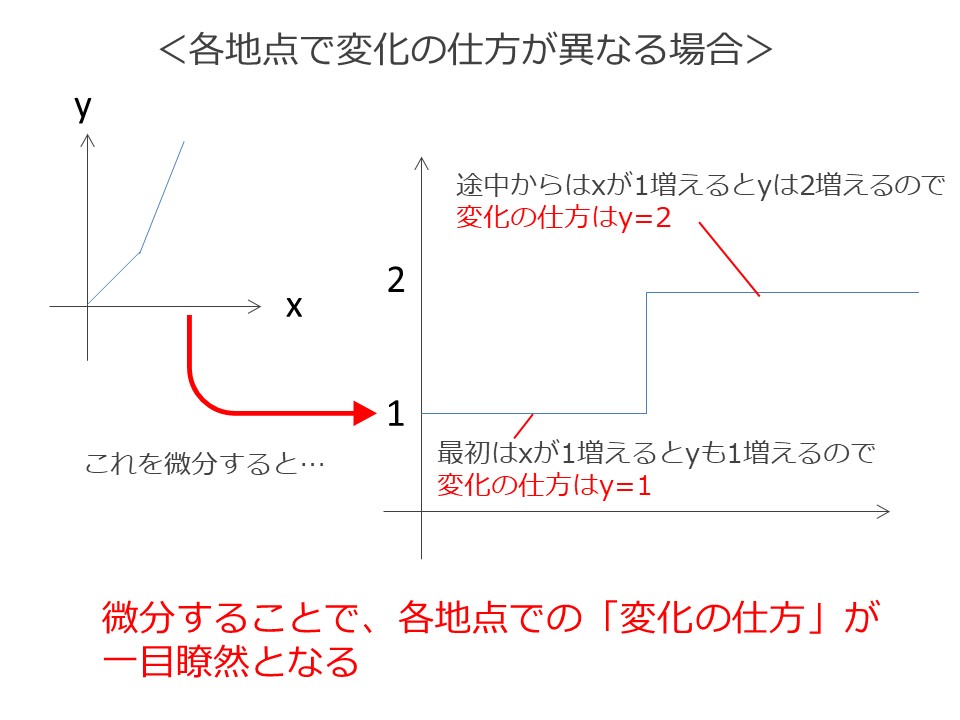
このように、変化するものを微分することで、そのものの「各瞬間での変化の仕方」が一目瞭然となるわけです。
ここが、微分が実社会で役に立っている1番のポイントです。
微分が何の役に立っているのか
先ほど説明したとおり、微分をすることで、「変化するものの、各瞬間の変化の仕方」が一目瞭然となります。
これが、実社会でどのように役立っているか、いくつか例を挙げてみましょう。
【①ロボットアーム】
スタート時は0の位置にあるロボットアームを、10秒後に10の位置に動かします。
この時、安全のため、ロボットアームがなるべく急激に変化しないようにします。
理想の動かし方を設定するために、まず実際にロボットアームを動かしてみて、その結果を「微分」します。
微分した結果が、なるべく急激な変化になっていないパターン(=変化の仕方の変化が小さい)が今回目指す動かし方であることがわかります。
【②陸上選手の例】
陸上選手が走った結果(距離)を微分すると、その選手の各瞬間での変化の仕方、つまり各瞬間での速度がわかります。
これによって、その選手の走り方の癖(最初飛ばしすぎ、どこで速度が落ちる…)などが一目瞭然になり、走りの分析ができます。
これは陸上に限らず、例えばある物質の変化を観察して、それを微分すると各瞬間の変化の仕方がわかります。
通常であれば変化の仕方が一定である物質なのに、変化が一定でない場所があるとすると、そこで何らかの問題が発生していたり、その物質の重要な特性が示されている可能性などがわかります。
【③温度制御】
エアコンは室温が設定した温度になるように部屋を暖めたり、冷やしたりします。
この時、単純に温度だけに着目しているわけではなく、「温度の変化の仕方」にも着目しています。
例えば、設定温度を25℃にしていて、現在の室温が24℃になったとしましょう。
その時、前の観測時点と比較して、急激に温度が下がっている場合(変化量が大きい場合)、その後も急激に温度が下がっていくことが予想されます。
よってエアコンは強力に部屋を暖めることで、室温が25℃になるよう保とうとします。
一方、前の観測時点の比較して、少ししか温度が下がっていない場合(変化量が小さい場合)、その後も急激に温度が下がっていく可能性は低いため、エアコンはあまり無理をせず、少しの力で部屋を暖めれば、それで十分室温が25℃に保たれる、ということになります。
このように、時間ごとの温度の実際の変化を微分し「変化の仕方」に着目することで、部屋を効率的かつ安定的に温めている、ということです。
これらはほんの一例ですが、物事の実際の変化だけでなく「変化の仕方」に着目する微分が、世の中の様々な物事に使われているわけです。
微分の成り立ち
最後に、微分の成り立ちについてご紹介しておきます。
数学の一分野として発明された微分ですが、これが実社会で役に立ち始めたのが16世紀ころのヨーロッパ。
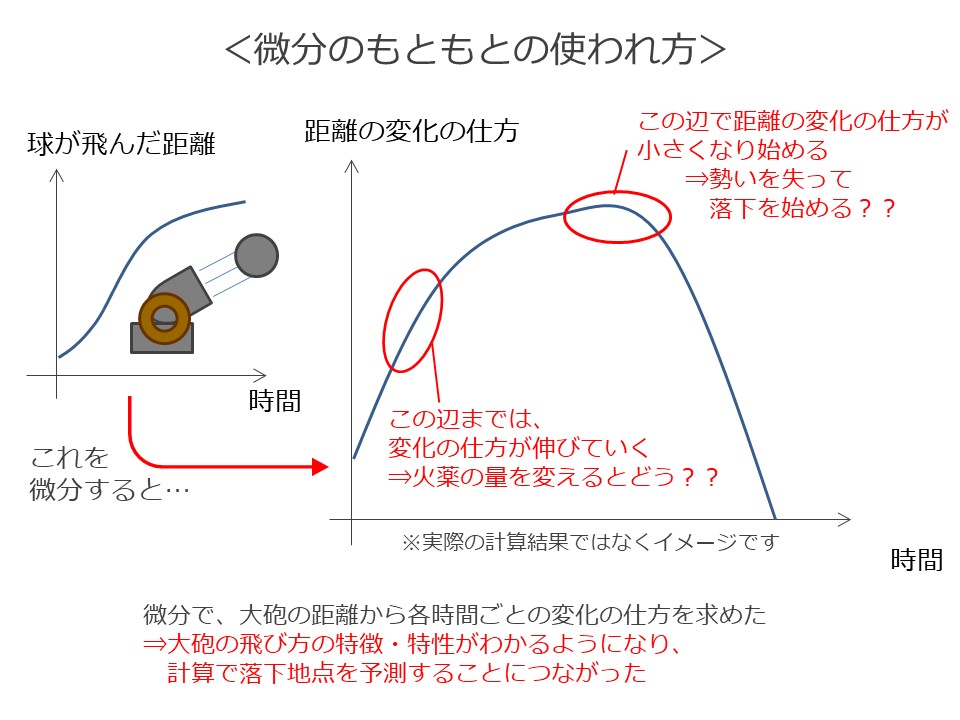
戦争において、大砲の球の着弾地点を計算で予測するのに使われました。
例えば、実際に球が飛んだ距離を微分することで、大砲の距離の変化の仕方、つまり大砲の飛び方の特性がわかるわけです。
下図はイメージですが、例えば
スタートから〇秒後までは変化の仕方が伸びていく、
〇秒後から変化の仕方が小さくなる⇒勢いを失って落下を始める
など、飛び方の特徴、特性がわかるようになり、これらを分析することで計算で球の着弾地点が予測できるようになっていったわけです。
こうして微分は数学の一分野から、金の成る木に変わり、現代でもさまざまな分野で活用されているというわけです。
今回は微分について説明しました。次回は積分についてご説明したいと思います。
微分積分とは何か、何に使われるのか② 積分編
