数学において多くの人がつまづきやすい単元である「三角関数」
サイン、コサイン、タンジェントという言葉は覚えていても、それが何を示しているのかはよくわからず、また、社会でどのように使われているのかも知らない方は多いのではないでしょうか。
そこで今回は、三角関数とは何かということから、社会でどのように役に立っているのかを説明していきたいと思います。
三角関数とは
三角関数というのは、
直角三角形の場合、1か所の角度が決まると、2辺の比は必ず一定の値になる
という規則です。
※比というのは、2つの数字の関係性を表したもの
例えばAさん(体重40kg)と、Bさん(体重80kg)の人の比は、40:80 とか、40/80 = 1/2 と表されます。
これは、Aさんの体重がBさんの体重の1/2であることを示します。
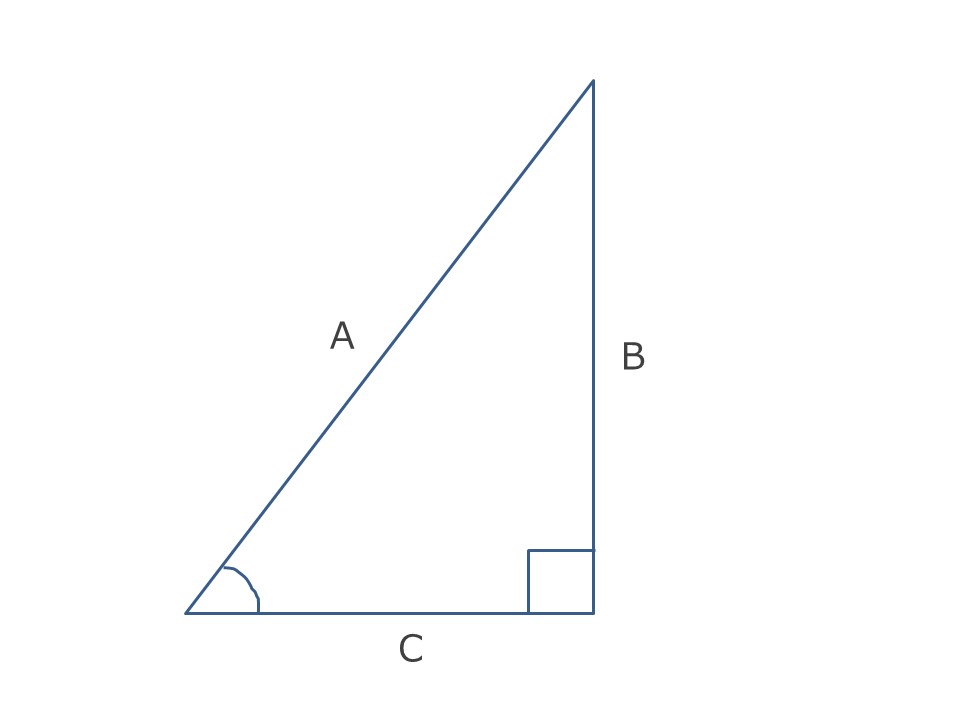
下図でいえば、
辺Aと辺Bの比(B/A)のことを「sin(サイン)」
辺Aと辺Cの比(C/A)のことを「cos(コサイン)」
辺Cと辺Bの比(C/B)のことを「tan(タンジェント)」
と呼んでいます。
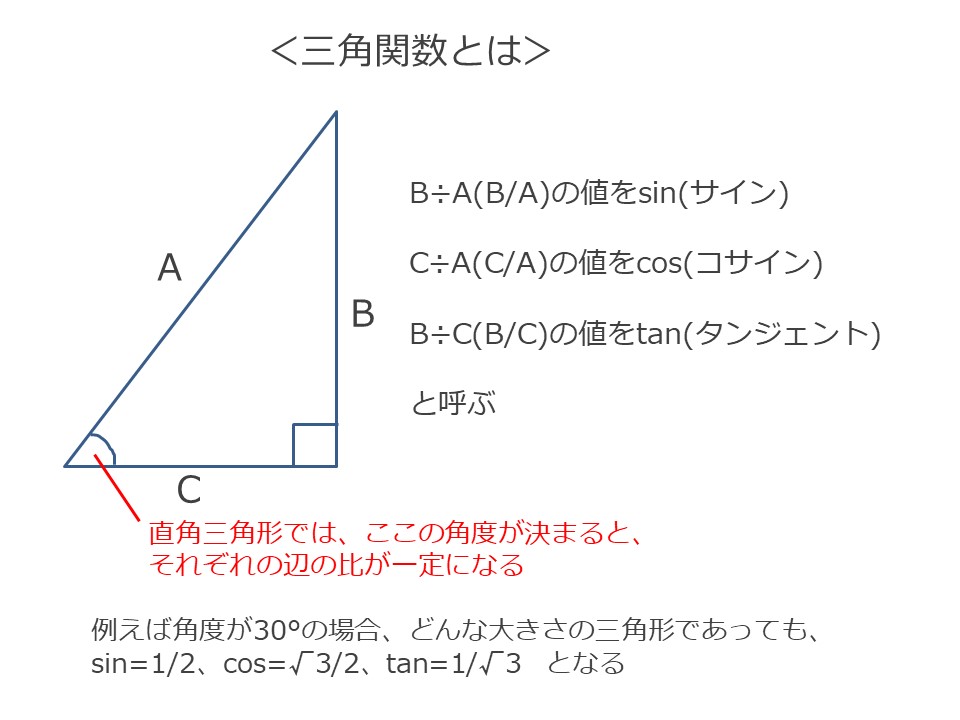
例えば、左下の角度が30°の場合、三角形がどんな大きさであっても、
BとAの関係性(B/A)つまりsinは1/2
CとAの関係性(C/A)つまりcosは√3/2
BとCの関係性(B/C)つまりtanは1/√3
と、決まった関係性(比)になります。
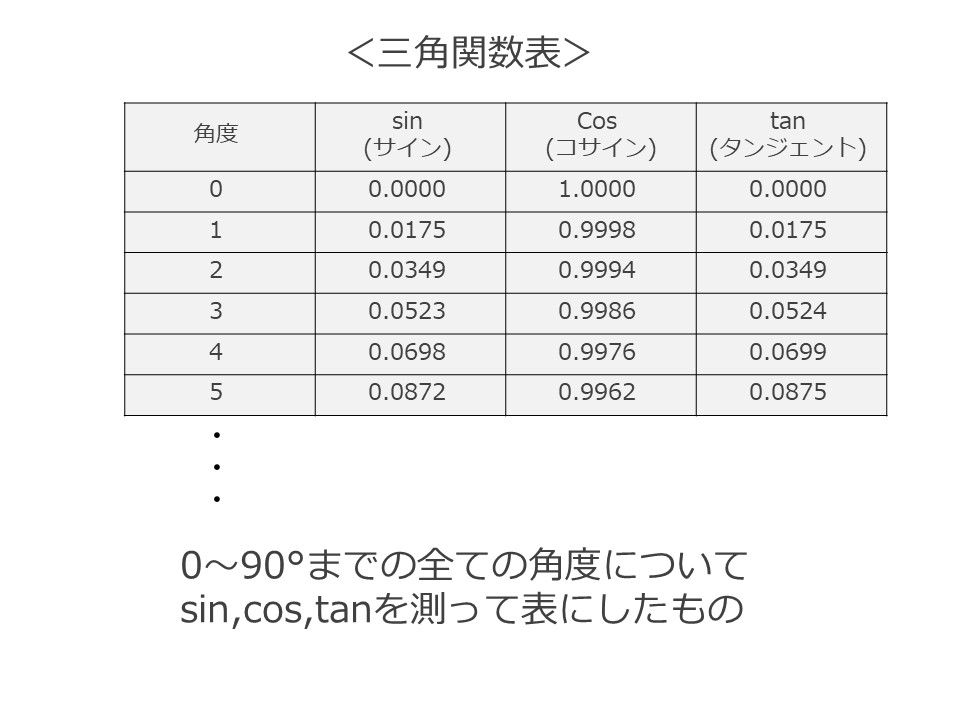
これらの比は、左下の角度が1℃変わるごとに変わりますが、昔の数学者(誰かは明確には不明)が、角度を1°ずつずらした三角形を書き、それら全ての角度について比を計算した表が「三角関数表」です。
現代の私たちは、その表を見れば、この角度の場合は、2辺の比はこの数値である、とすぐにわかるわけです。
これで、三角関数がどのようなものであるかは理解していただけたと思います。
続いて以下で、三角関数が社会でどのように使われているのか、何の役に立つのかをご紹介します。
三角関数は社会で何に使われているのか
三角関数の最も古典的な使われ方として、
直接測れないないものの長さを計算することができる
というものが一番メインの使われ方です。
先ほどの説明のとおり、直角三角形において、一か所の角度が決まれば、各辺の比は一定である、というのが三角関数でした。
つまり、辺と辺の関係性(比)はわかっているので、1つの辺の長さがわかれば、残りの辺の長さも計算できる、というわけです。
(例)AとBが1:2(A/B=1/2)の場合、Aが50だとすると、Bは100となる
この三角関数の特性を利用すれば、直接測れないものの長さも、直角三角形に当てはめることで計算できるようになります。
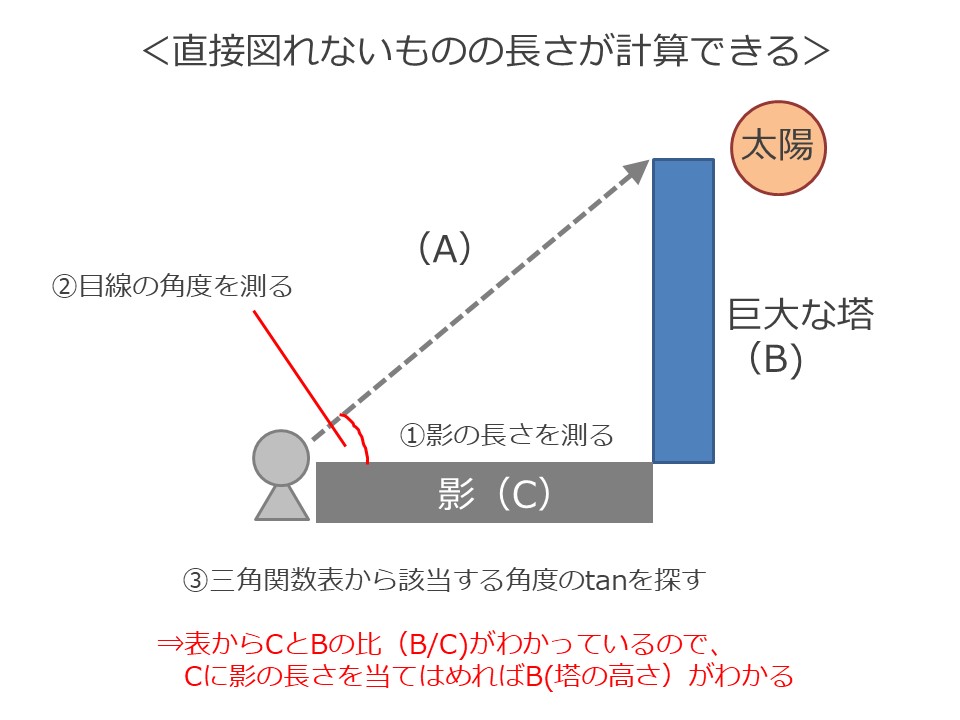
例えば、高すぎて直接図ることができない塔があるとします。
その塔の影は横向きなので直接図ることが可能です。
また、影の先端から塔の先端への角度は目線の角度を測ればわかります。
これで、直角三角形の角度と1辺の長さがわかったので、その角度のタンジェント(=CとBの比を表す)を三角関数表から探して、そこに影の長さを当てはめれば、塔の高さが計算できる、というわけです。
現代でも、上記のように高さがあったり、地形の問題で直接測ることができないような場所は三角関数を使って測量されています。
続いてもう1つ三角関数の使われ方を挙げてみましょう。
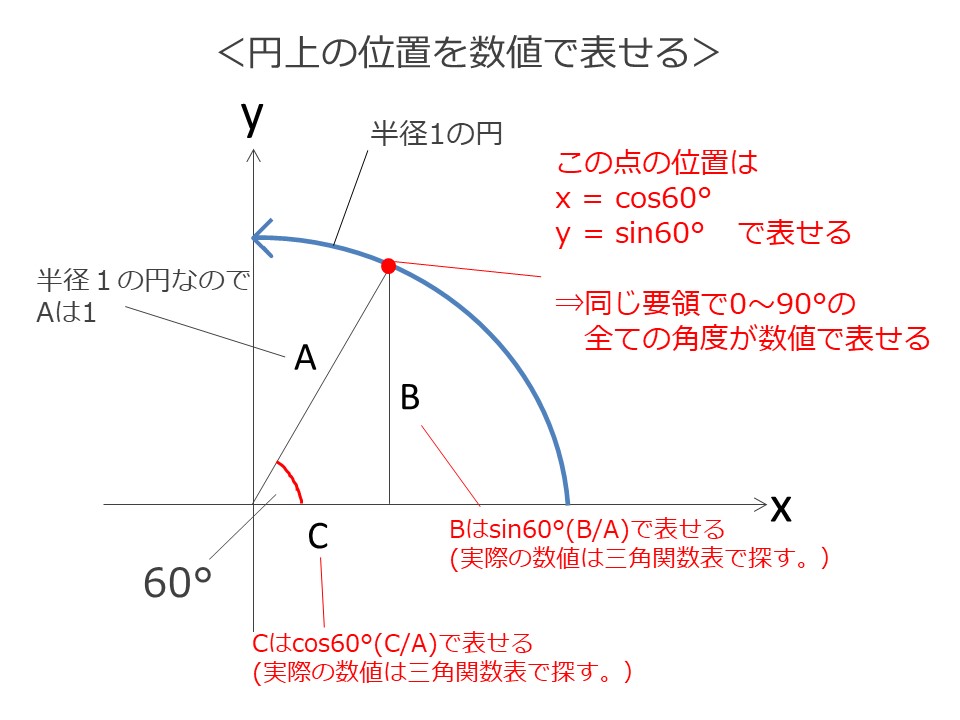
三角関数はXY座標において、円上の位置を表すことができます。
XY座標上の円を「半径1の円」として、0から円上の1点に向かう線をAとします。
また、円上の1点からX軸に向かって垂直な線Bを引きます。
すると、XY座標上に見慣れた直角三角形が現れます。
半径1の円なので、Aの長さは「1」とわかっています。
ここで角度が60°だとすると、
X軸の位置を表すCの長さはcos60°(60°の場合のC/A)
Y軸の位置を表すBの長さはsin60°(60°の場合のB/A)
で表すことができる、というわけです。
(実際の数値は三角関数表で探します。)
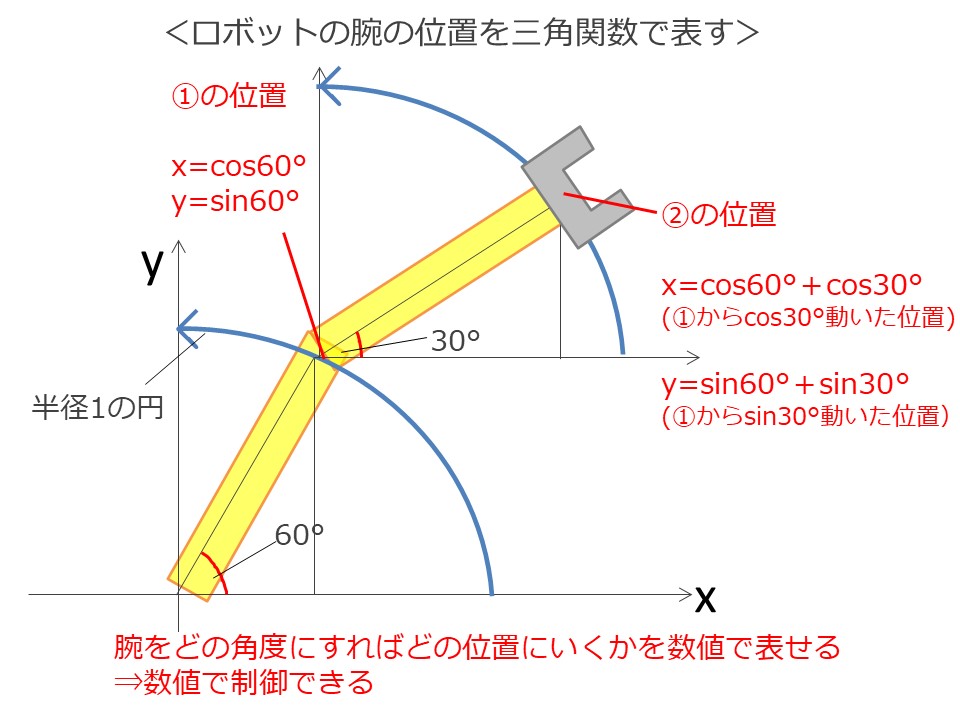
これが実社会で役に立っている例として、「ロボットアームの角度と位置を表す」というものがあります。
円の半径をロボットアームに当てはめると、ロボットアームの角度によって、その位置がsinとcosで表すことができます。
下の図でいえば、1つ目の関節(肩)を60°に曲げた場合の先端の位置①を
x=cos60°
y=sin60°
と表せます。
続いて2つ目の関節(肘)を30°に曲げた場合の先端の位置②は、先ほどの①からさらにx軸にcos30°、y軸にsin30°動いた位置ですので、
x = cos60°+cos30°
y = sin60°+sin30°
と表すことができるわけです。
三角関数の特性である、「角度が決まれば辺の比が決まる」を活用することで、ロボットアームの角度が決まればその位置を決めることができるということです。位置を数字で表すことができることで、コンピューターはその位置を制御ができる、というわけです。
(コンピューターはあいまいな言葉では位置を制御できません。数値で位置を1点に定める必要があります)
以上、三角関数とは何か、ということから、実際に社会にどのように役に立っているかをご紹介しました。
使い道はこれだけではありませんが、この2つの例だけでも、実社会で非常に有用なツールであることがわかっていただけたかと思います。
数学の授業では一見何の役に立つかわからず、意味不明な呪文にしか聞こえなかった三角関数も、このように実社会で必要とされる知識である、ということがわかれば理解しようとする意欲がわくのではないでしょうか。
